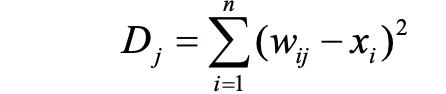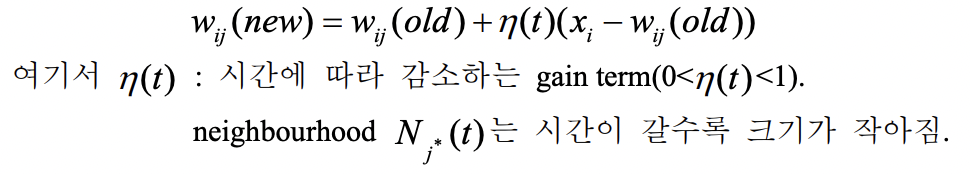본 < 지능형 시스템 > 시리즈는 부산대 정보컴퓨터공학과 차의영 교수님의 '지능형 시스템' 강의에서 배운 내용을 바탕으로 작성합니다.
| 신경회로망의 학습 방법 | 예시 |
|---|---|
| 1. 지도 학습 | Rosenblatt의 퍼셉트론(단층), 다층 퍼셉트론 |
| 2. 비지도 학습 | SOM |
| 3. 고정 가중치 | 홉필드 네트워크 |
🧠 Kohonen Network
- SOM (자기조직화지도) 이다.
- 임의의 시작점에서부터 특징 지도를 구조화할 수 있는 two-layer 네트워크이다.
- 학습 결과의 map은 네트워크에 주어지는 패턴들 사이의 관계를 나타낸다.
- 주어진 입력 패턴에 대해 정확한 해답을 가르쳐주지 않고 자기 스스로 학습하는 비지도 학습이다.
✔️ 기본 구조
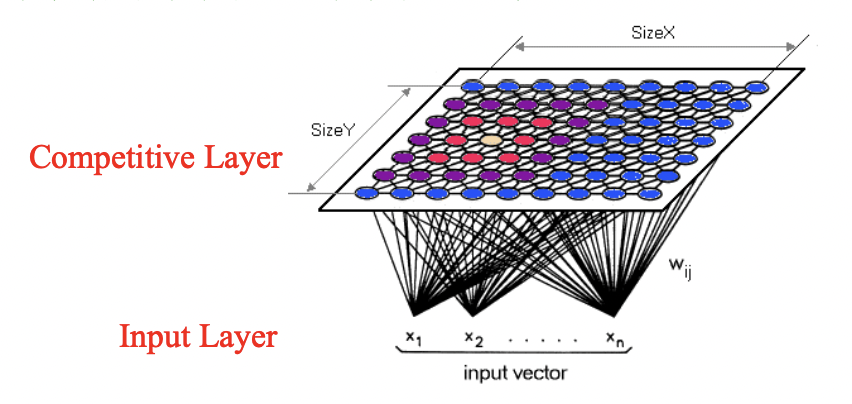
├── input layer
| : 입력 패턴을 받아들이는 층
|
└── competitive layer
: 일반적으로 2차원의 fully connected grid
: 입력X가중치 한 후, 단 하나의 승자 unit을 찾기 위해 경쟁.➡️ 전체적인 동작이 comptetive learning paradigm와 유사하나, 수정할 weight 를 선택하는 방법과 식 등이 다름.
✔️ 조건
뉴런의 연결강도 벡터를 임의값으로 적당히 초기화한다.
연결강도 벡터와 입력 벡터가 0~1사이의 정규화된 값이다.
🧠 Kohonen Network Algorithm
(1) 연결강도를 0~1 사이의 작은 값으로 초기화한다.
(2) 새로운 입력을 제시한다.
(3) 입력과 각 출력 unit j 사이의 거리 Dj를 계산한다.
(4) 최소거리 Dj 인 출력 뉴런 j* 을 선택한다.
(5) Neighbourhood size Nj*(t)에 의해 정의되는 neighbour 와 unit j* 을 위한 weight를 수정한다.
새로운 가중치 = 이전 가중치 + 변화량
(6) 단계 (2)로 돌아감.
✔️ 학습률 Learning rate
 학습률 계수는 계산 거듭할수록 점점 작아진다.
학습률 계수는 계산 거듭할수록 점점 작아진다.
👩🏫 예제
문제 : SOM 으로 4개의 벡터 군집화하기
< SOM 으로 4개의 벡터 군집화하기 >
- 4개의 벡터 : (1,1,0,0) (0,0,0,1) (1,0,0,0) (0,0,1,1)
- 최대 군집 수 : m = 2
- 학습률 :
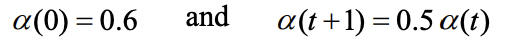
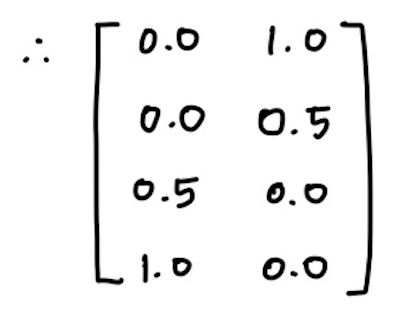
- 초기 가중치 행렬 :
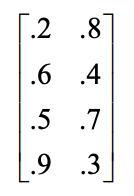
- 초기 반경 : R = 0
경쟁층이 단지 2개의 노드 뿐이기 때문에 이웃 개념은 없다고 가정한다.
풀이

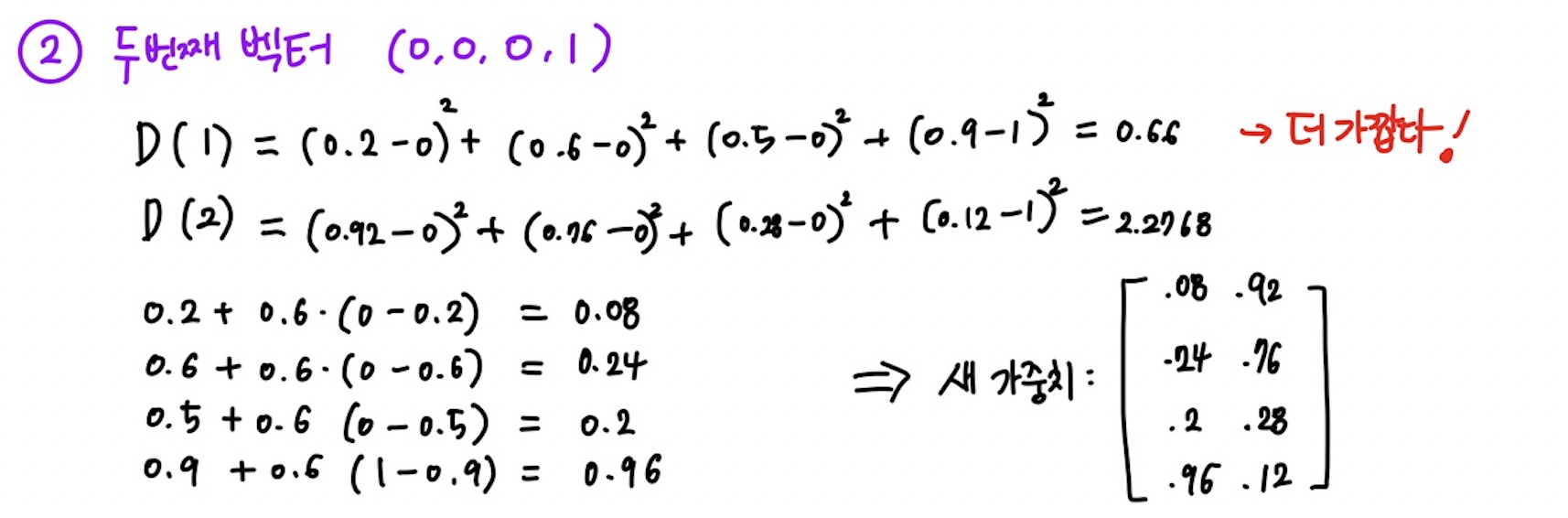
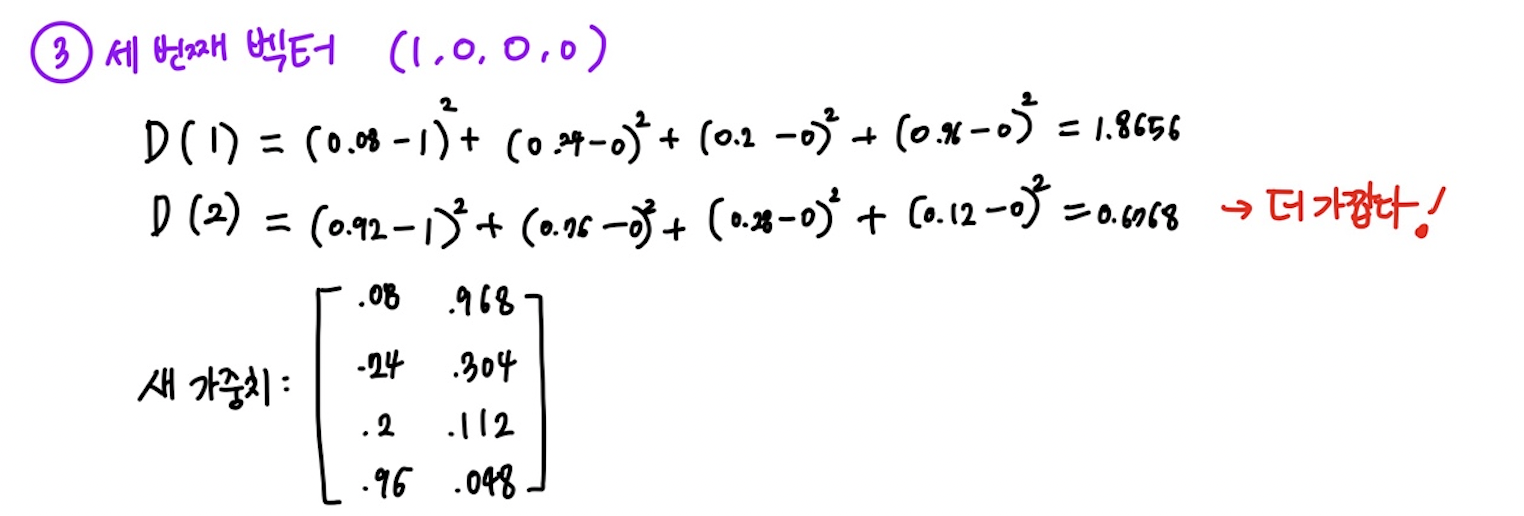
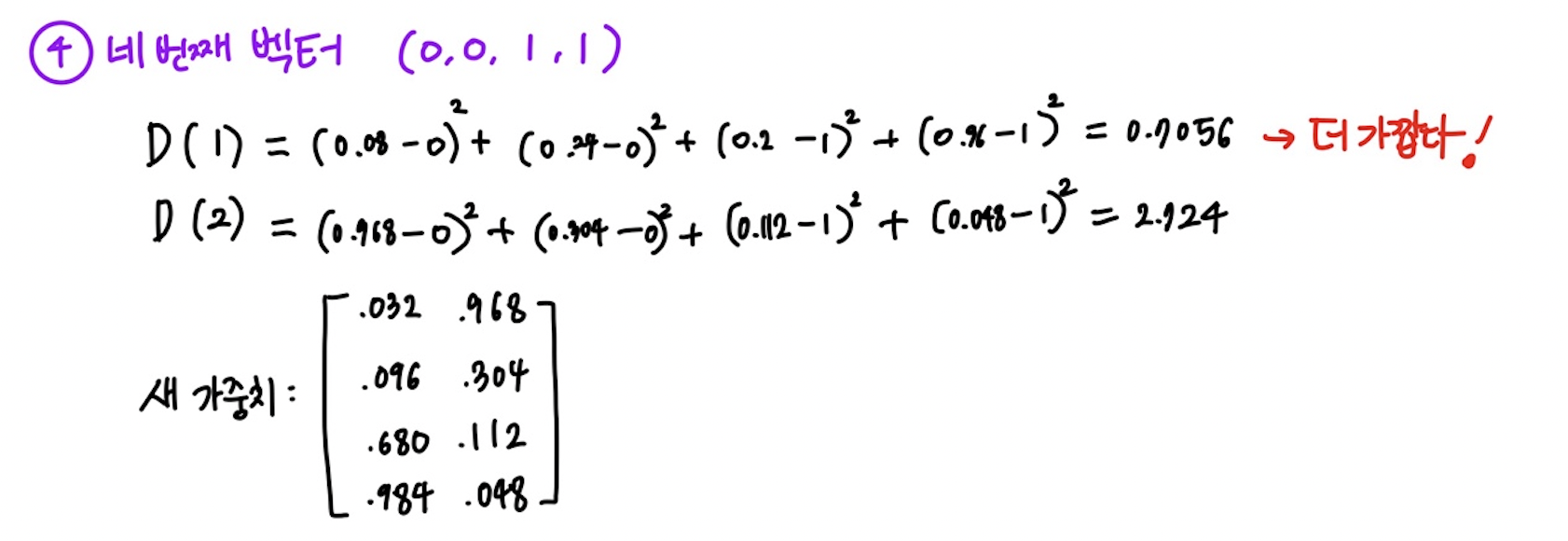
➡️ 지금까지 한 번의 학습이 끝났으므로 학습율을 감소시킨다.
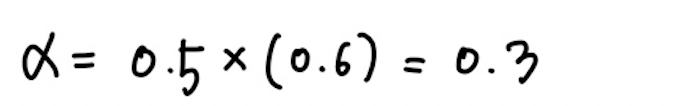
- 가중치 공식도 수정한다.
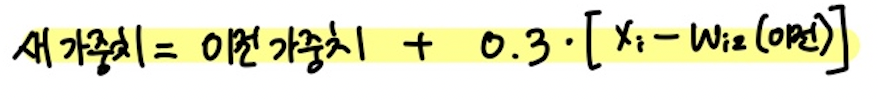
➡️ 이런 방법으로 반복 횟수를 계속 수행하게 되면, 결국 결과는 각 cluster에 속하는 벡터들의 평균값이 된다.
문제 : Character Recognition
< Character Recognition >
3가지 다른 폰트를 Kohonen self-organizing map을 이용하여 분류하는 예제
총 세가지 방법
- No topological structure
- Linear structure
- Diamond structure
풀이
- No topological structure
: 25개의 노드를 경쟁층에 두고 승자 뉴런 J만을 학습 - Linear structure
: 승자 노드 J와 이웃 노드 J-1, J+1을 학습 - Diamond structure
: 승자 노드 J와 4-neighborhood 노드를 학습
| 신경망 그림 | 결과 | |
|---|---|---|
| 1 | 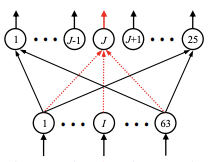 ➡️ j 만 고친다 |
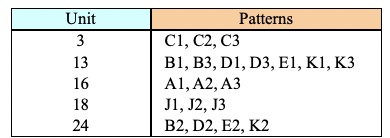 ➡️ 클러스터 5 군데 |
| 2 | 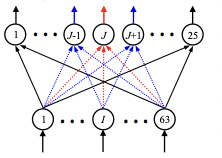 ➡️ j 주변도 고친다 |
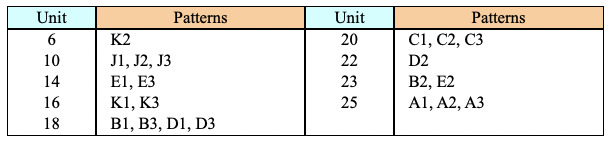 ➡️ 클러스터 9군데 |
| 3 | 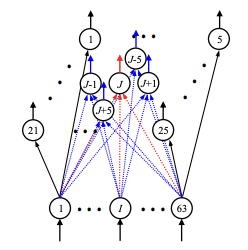 ➡️ 주위 네 개를 학습 |
 ➡️ 더욱 정교하게 |
👩🏫 Quiz
Question )
영문자 26개 + 숫자 10개 = 총 36개의 input 값을 학습시킨다고 하자. 각각 얼마나 많은 뉴런이 필요할까 ?
- Single-layer Perceptron
- Hopfield Network
- SOM
Answer )
- 6 개
2의 5승 < 36 < 2의 6승
따라서 최소 뉴런의 개수는 6개이다. - 241 개
M < 0.15 N
36/0.15 = 240 < N
따라서 241 개이다. - 36 개
최소 36개보다 크면 보기가 좋고, 골고루 퍼질 공간이 더 넓을수록 좋다.
Question )
그러면 위의 경우의 예에서 Weight 행렬의 크기는 ? 이때 문자 디자인을 Hopfield Network의 20X16 = 320 을 기준으로 하자.
- Single-layer Perceptron
- Hopfield Network
- SOM
Answer )
- 320 X 6 개
- 320 X 20 X 16 개
최소 뉴런 개수가 241개 였다.
20X13, 20X14 등..있지만, 20X16을 채택한다면 320X20X16이 된다. - 320 X 10 X 10 개
최소 뉴런 개수가 36개 였다.
2차원 경쟁층을 고려하여 10X10 을 채택한다면 320X10X10 이 된다.
'🤖 Artificial Intelligence > Intelligent System' 카테고리의 다른 글
| [지능형 시스템] Chapter 7. 신경회로망의 분류 ( Taxonomy ) (0) | 2023.06.10 |
|---|---|
| [지능형 시스템] Chapter 6. 오차역전파법 ( Backpropagation ) (0) | 2023.06.09 |
| [지능형 시스템] Chapter 4. 홉필드 네트워크 Hopfield Net (0) | 2023.06.07 |
| [지능형 시스템] Chapter 3. 초기 퍼셉트론, 아달린(Adaline), 최소평균제곱법(LMS) (2) | 2023.06.06 |
| [지능형 시스템] Chapter 2. 인공신경망의 응용 (0) | 2023.06.05 |