SIFT (Scale Invariant Feature Transform)

💡 극값과 유사한 Keypoint를 찾아 대표 방향(θ)을 정한 후, Keypoint 주변 정보를 히스토그램 벡터로 요약 표현하는 알고리즘.

 

어떤 사물을 찍을 때, 카메라 각도나 거리가 달라져도 같은 물체임을 알아볼 수 있도록 하는 "특징"을 추출하기 위한 방법.

즉, scale, roatation에 invariant한 특징점 (keypoint)를 찾는 것이 목표.

1. Making Scale-Space

• 이미지를 여러 크기로 변환 (Scale 조정)해서 특징점 찾기.
• 각 scale마다, 가우시안 블러를 다양하게 적용 (\( \sigma \) 조정)
  

  

2. Computing DoG images

• 각 scale 단계에서, 인접한 블러 이미지끼리 빼서 Difference of Gaussian (DoG) 이미지 생성.
  

  

3. Finding Keypoints

• DoG에서 극댓값/극솟값(local extreme) 찾음. \(D(x)\)를 \(x\)에 대해 미분 후, 0으로 둬서 구함
  

  

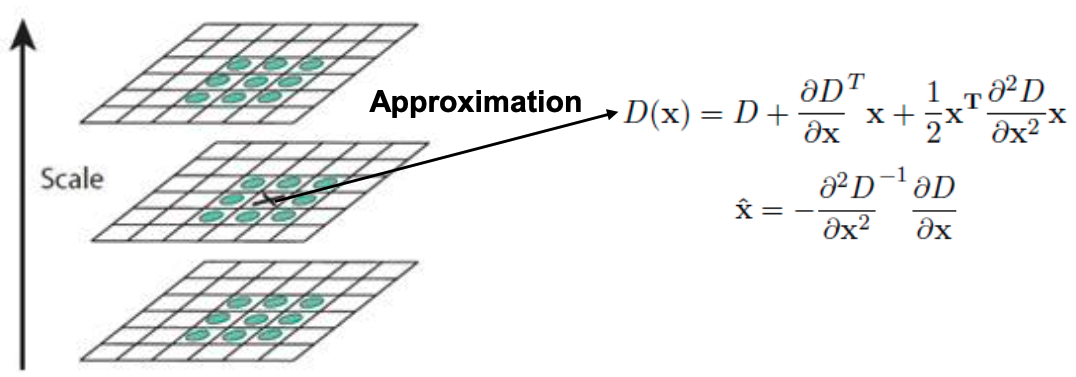
4. Keypoint Refinement

• local extreme 중에서 다음을 제거:
  1. DoG 값이 너무 작은 것. If \(|D(\hat{x})| < \) threshold, discard key.
  2. Flat (양쪽 gradient \(\downarrow\)), Edge (한쪽 gradient만 \(\uparrow\)).
• 즉, Corner만 남김.
  

5. Keypoint Orientation

• 남은 Keypoint "주변의" gradent 방향과 크기를 계산.
  • magnitude: \(m(x,y) = \sqrt{(L(x+1,y)-L(x-1,y))^2+(L(x,y+1)-L(x,y-1))^2}\)
  • angle: \(\theta(x,y) =\tan ^{-1} (\frac{L(x,y+1)-L(x,y-1)}{L(x+1,y)-L(x-1,y)}) \)
• Keypoint에 가까운 픽셀은 더 중요하므로, "gradient 크기 \(m\)"에 가우시안 가중치 \( w = \exp (-r^2 / 2 \sigma^2_w) \)를 곱함.
• 0°~360° 범위를 10° 간격으로 나눠서 36개의 bin 히스토그램 만듦.
  • 모든 픽셀의 가중된 "gradient 크기"를 해당 bin에 누적.
• 가장 큰 bin의 방향을 대표 방향(\( \theta \))으로 선택.
  • 만약 다른 bin이 최대치의 80% 이상이면, 그방향도 추가로 keypoint에 할당.
• 따라서 이제, Keypoint는 \((x, y, \sigma, \theta)\)를 가짐. -> 즉, 기준 축 (\(\theta\))가 정해짐.
• 이후, Descriptor를 계산할 때, 이 기준축에 맞춰 패치를 돌려놓고, 정규화된 방향 체계에서 gradient 패턴을 기록함.

6. Keypoint Descriptor

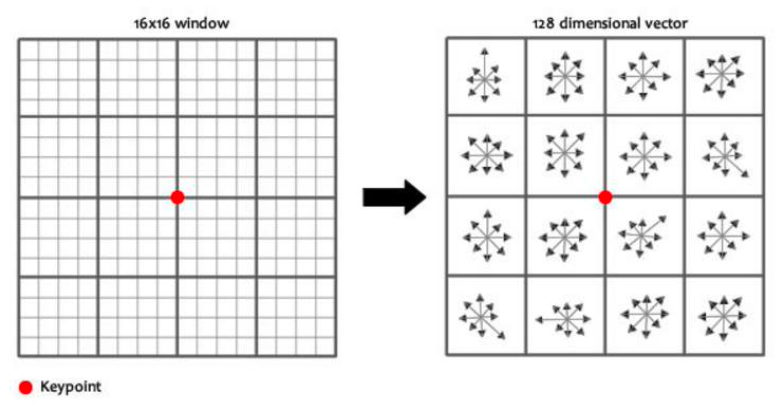
1. 키포인트 주변 패치 잡기

• 하나의 keypoint가 있다고 하자.
• keypoint를 중심으로 "16×16 픽셀 패치"를 선택한다.
• 각 픽셀에서 gradient의 크기와 방향을 계산한다.
  • 픽셀 단위 정보 그대로 쓰면 차원이 크고 노이즈에 민감.
  • 따라서 간결한 표현으로 요약해야 함.

2. 셀 단위로 요약하기

• "16×16 픽셀 패치"를 "4×4 셀"로 나눈다.
  • 즉, 한 셀은 4×4 = 16 픽셀을 포함한다.
• 각 픽셀의 gradient 방향은 연속적인 값(0°~360°)이므로, 이를 8개의 방향 bin (0°, 45°, …, 315°) 중에 분배한다.
  • 한 픽셀의 gradient는 가장 가까운 두 방향 bin에 가중치를 나눠서 누적됨.
• 결과적으로, 한 셀은 16개 픽셀의 gradient 정보를 모아 8차원 방향 히스토그램 벡터로 요약됨.

3. 최종 Descriptor 완성

• 총 4×4 = 16개의 셀이 있으므로, 각 셀의 8차원 벡터를 연결(concatenate)한다.
• 따라서 한 keypoint의 descriptor는
  $$
  16 \text{ (셀)} \times 8 \text{ (방향 bin)} = 128 \text{차원 벡터}
  $$
• 이 128D descriptor가 keypoint의 “지문” 역할을 하며, 다른 이미지에서도 같은 keypoint를 인식할 수 있게 한다.